Question

A fast-food restaurant buys hamburger buns from a national bakery supplier. The daily usage of buns at the restaurant is normally distributed with an average of 160 and standard deviation of 10. It takes 4 days for the supplier to deliver. The purchasing agent at the restaurant has established a 99.7% service level.

a) The Safety Stock and Reorder Point for the restaurant (in whole numbers). A fast-food restaurant buys hamburger buns from a local bakery. To estimate its costs, the restaurant assumes now those buns are used at the constant rate of 100 per day and are purchased at $0.025 per bun. It costs $1 for each order placed and the annual inventory holding cost per unit is 25% of the unit purchase cost.
b) How much should be ordered each time to minimize the restaurant’s total annual costs?c) And what is the length of order cycles (i.e. time between orders) in days? Assume the restaurant operates 360 days per year.

Answer 1

Thus, from the calculations below;

The safety stock = 55

The reorder point = 695

quantity required to be ordered in order to reduce and minimize total annual cost for the restaurant = 3394 buns

The order cycles length = 34 days

Step-by-step explanation:

From the given information:

The average demand (d) = 160

The standard deviatiion
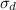`\sigma_d` = 10

Lead time = 4 days

Service level = 99.7% = 0.997

From the Standard Normal Curve; the z value at 99.7% = 2.75

The annual demand (D) = 36000

Ordering cost = $1

Unit purchased Cost = $0.025

The holding cost for the annual inventory = 25% of 0.025 = 0.00625

The reorder point can be determined by using the formula:

`= \bar d * Lead \ time +z* \sigma_d * √(LT)`

`\mathbf{ = 160\ *4+2.75 *10 *√(4)}`

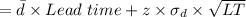
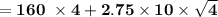
= 695

The safety stock SS =
`z * \sigma_d * √(LT)`

`= 2.75 * 10 * √(4)`

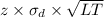
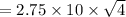
= 55

The economic order quality =
`\sqrt{2 * D * (ordering \ cost )/(annua l\ holding \ cost)}`

`= \sqrt{2 * 36000 * (1 )/(0.00625)}`

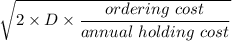
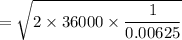
=3394.11

The order cycle length =
`(EOQ)/(D)* 360`

`= (3394.11)/(36000)* 360`

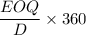
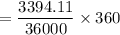
= 33.94

≅ 34 days