Question

Repost bcs last one wasnt clear BUT PLEASE HELPP 5 MINS LEFT

Answer 1

`m =13`

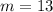
Explanation:

Given

The attached dataset

Required

The mean absolute deviation

First, calculate the mean

`\bar x = (\sum x)/(n)`

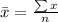
So, we have:

`\bar x = (42+40+39+76+71+55+68+65)/(8)`

`\bar x = (456)/(8)`

`\bar x = 57`

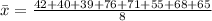
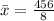
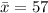
The mean absolute deviation (m) is:

`m =(1)/(n) \sum|x - \bar x|`

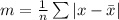
So, we have:

`m =(1)/(8) (|42 - 57| + |40 - 57| + |39 - 57| + |76 - 57| + |71 - 57| + |55 - 57| + |68 - 57| + |65 - 57|)`

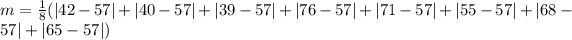
Using a calculator, we have:

`m =(1)/(8) (|-15| + |-17| + |-18| + |19| + |14| + |-2| + |11| + |8|)`

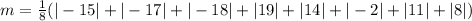
Remove absolute bracket

`m =(1)/(8) (15 + 17 + 18 + 19 + 14 + 2 + 11 + 8)`

`m =(1)/(8) *104`

`m =13`

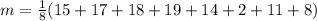
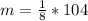
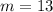
The mean absolute deviation is 13