Question

Please help me out tired want to sleep

Answer 1

The approximate area by Riemann Sum of the curve is represented by
`A = 0.4\cdot \Sigma\limits_(t = 1)^(n) [2\cdot (2+0.4\cdot t)^(3) - 4]`.

Explanation:

The area below the curve is estimated by the concept of Riemann Sum with right endpoint rectangles, which is defined by the following formula:

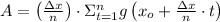`A = \left((\Delta x)/(n) \right) \cdot \Sigma \limits_(t = 1)^(n) g\left (x_(o) + (\Delta x)/(n)\cdot t \right)` (1)

Where:

`A` - Area below the curve, in square units.

`n` - Number of rectangles, no units.

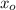`x_(o)` - Lower bound of the interval, in units.

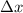`\Delta x` - Length of the interval, in units.

`t` - Summation index.

If we know that
`g(x) = 2\cdot x^(3) - 4`,
`n = 10`,
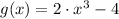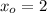`x_(o) = 2` and
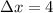`\Delta x = 4`, then the area below the curve is represented by the following equation:

`A = 0.4\cdot \Sigma\limits_(t = 1)^(n) [2\cdot (2+0.4\cdot t)^(3) - 4]`