Given:
The table for a geometric sequence.
To find:
The formula for the given sequence and the 10th term of the sequence.
Solution:
In the given geometric sequence, the first term is 1120 and the common ratio is:
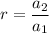
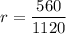
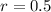
The nth term of a geometric sequence is:
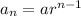
Where a is the first term and r is the common ratio.
Putting
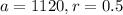 , we get
, we get
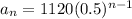
Therefore, the required formula for the given sequence is
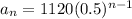 .
.
We need to find the 10th term of the given sequence. So, substituting
 in the above formula.
in the above formula.
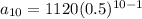
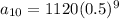
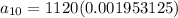
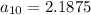
Therefore, the 10th term of the given sequence is 2.1875.