Question

Let f(x)=-4(2)^x. The graph of g(x)=f(x)+k is shown below. Identify the value of k.

Answer 1

Given:

The function is:

`f(x)=-4(2)^x`

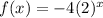
The graph of the function
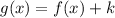`g(x)=f(x)+k` is given.

To find:

The value of k.

Solution:

We have,

`f(x)=-4(2)^x`

`g(x)=f(x)+k`

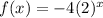
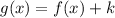
Using these two functions, we get

`g(x)=-4(2)^x+k`

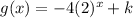
From the given graph it is clear that the graph of g(x) passes through the point (0,2). It means the point (0,2) satisfies the function g(x).

Substituting
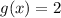`g(x)=2` and
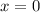`x=0` in the above function, we get

`2=-4(2)^0+k`

`2=-4(1)+k`

`2=-4+k`

`2+4=k`

`6=k`

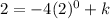
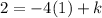
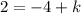
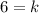
Therefore, the value of k is 6.