Question

The center of a circle is placed on the origin of a coordinate plane as shown below. The radius of the circle is 10 units. If the point (-6, y) lies on the circle, what is y?​

Answer 1

(-6, 8)

Explanation:

Since the radius is 10 units and the center is on the origin of the circle, the distance from the origin to the point (-6, y) must be 10.

We can use the distance formula given by:

`d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

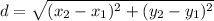
We will let the point (-6, y) be (x₂, y₂) and the origin point (0, 0) be (x₁, y₁). The distance is 10. Substitute:

`10=√(((-6)-(0))^2+((y)-(0))^2)`

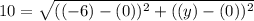
Simplify:

`10=√((-6)^2+(y)^2)`

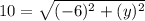
Square both sides and simplify:

`100=36+y^2`

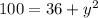
Solve for y:

`y^2=64`

Take the square root of both sides:

`y=\pm√(64)=\pm 8`

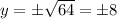
Since our point is in QII, y must be positive. Hence, we will use the positive case. So, y = 8.

Our point is (-6, 8).