4. Using the Method of Completing the square, find the zeroes of the following function to the nearest hundredth. F(x)=2x^2+12x+5

Question

asked May 8, 2022 5.6k views

1 Answer

Kandha · Answer 1 · 2022-05-14T03:38:47+0000

Given:

The function is:

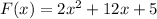
F(x)=2x^2+12x+5

To find:

The zeroes of the given function by using the Method of Completing the square.

Solution:

We have,

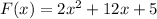
F(x)=2x^2+12x+5

It can be written as:

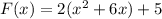
F(x)=2(x^2+6x)+5

By Method of Completing the square add and subtract square of half of coefficient of x in the parenthesis.

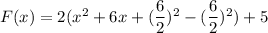
F(x)=2(x^2+6x+((6)/(2))^2-((6)/(2))^2)+5

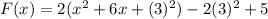
F(x)=2(x^2+6x+(3)^2)-2(3)^2+5

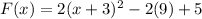
F(x)=2(x+3)^2-2(9)+5
$[\because (a+b)^2=a^2+2ab+b^2]$

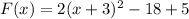
F(x)=2(x+3)^2-18+5

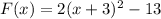
F(x)=2(x+3)^2-13

For zeroes, F(x)=0.

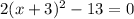
2(x+3)^2-13=0

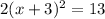
2(x+3)^2=13

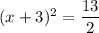
(x+3)^2=(13)/(2)

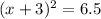
(x+3)^2=6.5

Taking square root on both sides, we get

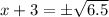
$x+3=\pm √(6.5)$

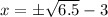
$x=\pm √(6.5)-3$

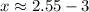$x\approx 2.55-3$ and
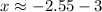
$x\approx -2.55-3$

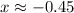$x\approx -0.45$ and
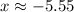
$x\approx -5.55$

Therefore, the zeroes of the given function are -0.45 and -5.55.