Answer:
The answer is f^-1(x)=0^3
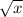 +2
+2
Explanation: Now we just change y back to f(x) and add a 0−1 to write it in inverse notation We begin with f(x)= x 3−2 . To find the inverse of any equation, just switch x and y No, before we do that, I'm going to change the equation. I'm going to rename f(x) to y , just so that I don't have to deal with the parentheses or anything. Now, all I have to do is change what f (x) is called, not it's actual value. Anyways, we have y = x 3 − 2 Now we switch x and y and then solve for y Now we've got x = y 3−2 If we add 2 on both sides we have x + 2 = y 3 Now we just need to get y as simple as possible, which we'll do by cube rooting both sides of the equation. That leaves us with y=0 3√x+2 Now we just change y back to f(x) and add a 0−1 to write it in inverse notation