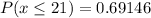Question

asked Feb 25, 2022 47.3k views

1 Answer

Sajan Parikh · Answer 1 · 2022-02-28T20:05:31+0000

Answer:

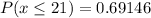
$P(x \le 21) = 0.69146$

Explanation:

The missing parameters are:

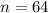n = 64 --- population

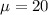$\mu = 20$ --- population mean

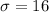$\sigma = 16$ -- population standard deviation

Required

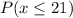
$P(x \le 21)$

First, calculate the sample standard deviation

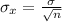
$\sigma_x = (\sigma)/(\sqrt n)$

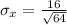
$\sigma_x = \frac{16}{\sqrt {64}}$

$\sigma_x = (16)/(8)$

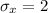
$\sigma_x = 2$

Next, calculate the sample mean
$\bar_x$

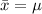
$\bar x = \mu$

So:

$\bar x = 20$

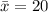
So, we have:

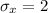
$\sigma_x = 2$

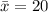
$\bar x = 20$

x = 21

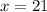
Calculate the z score

$x = (x - \mu)/(\sigma)$

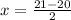
x = (21 - 20)/(2)

x = (1)/(2)

x = 0.50

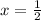
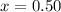
So, we have:

$P(x \le 21) = P(z \le 0.50)$

From the z table

$P(z \le 0.50) = 0.69146$

So:

$P(x \le 21) = 0.69146$

Please log in or register to add a comment.