Question

Element X is a radioactive isotope such that every 24 years, its mass decreases by

half. Given that the initial mass of a sample of Element X is 70 grams, how long
would it be until the mass of the sample reached 61 grams, to the nearest tenth of a
year?

Answer 1

Explanation:

We get to use the simple version of the half life equation:

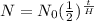`N=N_0((1)/(2))^{(t)/(H)` where N is the amount of radioactive element left after a specific number of years,

N0 is the initial amount of the element,

t is the number of years (our unknown), and

H is the Half life of the element. For us,

N is 61

N0 is 70,

t is unknown,

H is 24 years. Filling in:

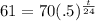`61=70(.5)^{(t)/(24)`. We begin by dividing both sides by 70 to get:

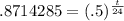`.8714285=(.5)^{(t)/(24)` and then take the natural log of both sides:

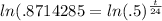`ln(.8714285=ln(.5)^{(t)/(24)` which allows us to bring down the exponent to the front on the right side:

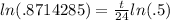`ln(.8714285)=(t)/(24)ln(.5)`. We divide both sides by ln(.5) to get:

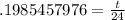`.1985457976=(t)/(24)` and then multiply both sides by 24 to get:

t = 4.8 years