Question

g if we want to calculate a confidence interval of the difference of two proportions what is the standard error (do not pool for this answer)

Answer 1

The standard error is
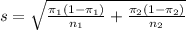`s = \sqrt{(\pi_1(1-\pi_1))/(n_1)+(\pi_2(1-\pi_2))/(n_2)}`, in which
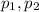`p_1,p_2` are the proportions and
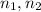`n_1,n_2` are the sample sizes.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

The standard error is:

`s = \sqrt{(\pi(1-\pi))/(n)}`

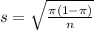
For the difference of proportions:

For proportion 1, the standard error is:

`s_1 = \sqrt{(\pi_1(1-\pi_1))/(n_1)}`

For proportion 2, the standard error is:

`s_2 = \sqrt{(\pi_2(1-\pi_2))/(n_2)}`

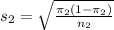
For the difference:

The standard error is the square root of the sum of the squares of each separate standard error. So

`s = \sqrt{(\sqrt{(\pi_1(1-\pi_1))/(n_1)})+(\sqrt{(\pi_2(1-\pi_2))/(n_2)})^2} = \sqrt{(\pi_1(1-\pi_1))/(n_1)+(\pi_2(1-\pi_2))/(n_2)}`

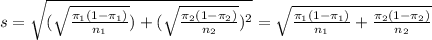
The standard error is
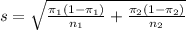`s = \sqrt{(\pi_1(1-\pi_1))/(n_1)+(\pi_2(1-\pi_2))/(n_2)}`, in which
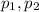`p_1,p_2` are the proportions and
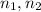`n_1,n_2` are the sample sizes.