Question

Is it possible to find two data sets A and B such that A has a greater median and mode, while B has a greater average and range? If you think the answer is yes, provide an example. If you think the answer is no, explain why not.

Answer 1

For a data set of N elements:

{x₁, x₂, ..., xₙ}

The median is the middle value (or the average of the two middle values)

The average or mean is:

`m = (x_1 + ... + x_n)/(N)`

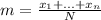
The mode is the value that is more repeated.

The range is the difference between the largest value and the smallest value.

Now, let's try to construct two sets A and B that meet the required conditions:

Let's suppose two sets of 5 values each:

A = {2, 2, 3, 4, 5}

The median of A is 3.

The range of A is = 5 - 2 = 3

The average of A is: (2 + 2 +3 +4 +5)/5 = 16/5

And the value "2" appears two times, so the mode is 2.

Now, let's try to find a data set B such that:

The mode is smaller than 2 (so for example, we can have a "1" that repeats two times)

The median is smaller than 3 (let's have a median equal to 2)

The average is larger than 16/5

The range is larger than 3

This is ratter simple:

B = {1, 1, 2, 6, 9}

The median of B is 2.

The mode of B is 1

The range of B is: 9 - 1 = 8

The average of B is: (1 + 1 + 2 + 6 + 9)/5 = 19/5

So, we just found an example for two data sets A and B such that A has a greater median and mode, while B has a greater average and range.

So the answer is yes, it is possible.