Question

Solve the simultaneous equations​

Answer 1

Explanation:

2x + 3y = 2

x = 2 - 3y /2

x + y = 0

substitute the value of x

`(2 \\- 3y)/(2)` + y = 0

2 - 3y + 2y = 0

2 = y

again,substitute the value of y

x = 2 - 3y / 2

=2 - 3*2 / 2

=2 - 6 / 2

=-2

Answer 2

x = 2, y = -2

Explanation:

This is an alternate way. You can also solve simultaneous equations using matrices. First, rewrite the simultaneous equations in matrix form.

`\displaystyle \large{\left[\begin{array}{ccc}2&3\\1&1\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] =\left[\begin{array}{ccc}2\\0\end{array}\right]}`

Let:

`\displaystyle \large{A= \left[\begin{array}{ccc}2&3\\1&1\end{array}\right]}\\\displaystyle \large{X = \left[\begin{array}{ccc}x\\y\end{array}\right]}\\\displaystyle \large{B =\left[\begin{array}{ccc}2\\0\end{array}\right]}`

So now we have
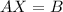`\displaystyle \large{AX = B}` and we have to solve for X which:

`\displaystyle \large{A^(-1)AX = A^(-1)B}\\\displaystyle \large{X = A^(-1) B}`

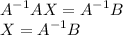
Where:

`\displaystyle \large{A^(-1)=(1)/(ad-bc)\left[\begin{array}{ccc}d&-b\\-c&a\end{array}\right]}`

**ad-bc is determinant of 2*2 matrices and shortened as det(var) or |var|**

Therefore, from A:

• a = 2
• b = 3
• c = 1
• d = 1

Find detA:

`\displaystyle \large\det A =`

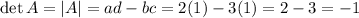
Therefore, detA = -1. Hence:

`\displaystyle \large{A^(-1)=-1\left[\begin{array}{ccc}1&-3\\-1&2\end{array}\right]}`

And
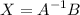`\displaystyle \large{X = A^(-1)B}`:

`\displaystyle \large{X = -1\left[\begin{array}{ccc}1&-3\\-1&2\end{array}\right] \left[\begin{array}{ccc}2\\0\end{array}\right] }`

Evaluate the matrices:

`\displaystyle \large{X = -1\left[\begin{array}{ccc}1 \cdot 2-3 \cdot 0\\-1 \cdot 2+2\cdot 0\end{array}\right] }\\\displaystyle \large{X = -1\left[\begin{array}{ccc}2-0\\-2+0\end{array}\right] }\\\displaystyle \large{X = -1\left[\begin{array}{ccc}2\\-2\end{array}\right] }\\\displaystyle \large{X = \left[\begin{array}{ccc}-2\\2\end{array}\right] }\\\displaystyle \large{\left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}-2\\2\end{array}\right] }`

Therefore, x = -2 and y = 2.