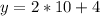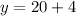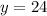Question

Consider the graph above. Write about a situation that could be modeled using this graph. In your response, use the prompts below to guide your thinking:

Answer 1

See Explanation

Explanation:

Given

See attachment for graph

Required

A situation that can be modeled by the graph.

The prompt and the response are as follows:

The type of function:

It is a linear function

The variables modeled in the function

The variables are x and y

The domain and the range

From the graph, we can see that x and y values are not limited to any constraints.

So, the domain and the range are:

`Domain: \{-\infty \le x \le \infty \}`

`Range: \{-\infty \le y \le \infty \}`

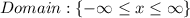
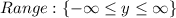
Question that could be
`answered`

The graph could be used to predict y value, given the x value.

Take for instance, find y when x = 10

The answer can be handpicked directly from the graph. However, the best way is to calculate the graph equation, first.

So, we have:

Pick any two points on the line of the graph

`(x_1,y_1) = (-2,0)`

`(x_2,y_2) = (0,4)`

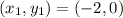
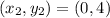
Calculate the slope (m)

`m = (y_2 - y_1)/(x_2 - x_1)`

`m = (4 - 0)/(0 - -2)`

`m = (4)/(2)`

`m =2`

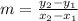
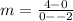
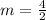
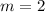
The equation of the graph is:

`y = m(x - x_1) + y_1\\`

So, we have:

`y = 2(x - -2) + 0`

`y = 2(x +2)`

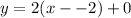
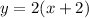
Expand

`y = 2x +4`

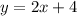
To solve for y when x = 10;

`y = 2 * 10 +4`

`y = 20 +4`

`y = 24`