Answer:
0.2835 = 28.35% probability that exactly two of them require warranty repairs.
Explanation:
For each TV, there are only two possible outcomes. Either they require warranty repairs, or they do not. The probability of a TV requiring warranty repairs is independent of any other TV, which means that the binomial probability distribution is used to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
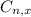 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
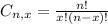
And p is the probability of X happening.
10% require repair to be done under the warranty during the first year service.
This means that
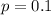
A particular dealership sells 18 such TV per week.
This means that

a) What is the probability that exactly two of them require warranty repairs?
This is
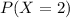 . So
. So

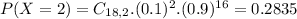
0.2835 = 28.35% probability that exactly two of them require warranty repairs.