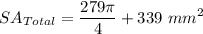Answer:
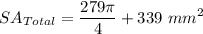
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
Geometry
Shapes
Congruency
- Congruent sides and lengths
Radius Formula:
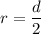
Surface Area of a Rectangular Prism Formula: SA = 2(wl + hl + hw)
- w is width
- l is length
- h is height
Surface Area of a Cylinder Formula: SA = 2πrh + 2πr²
Explanation:
Step 1: Define
Identify
[Rectangular Prism] w = 9 mm
[Rectangular Prism] l = 11 mm
[Rectangular Prism] h = 6 mm
[Cylinder] d = 9 mm
[Cylinder] h = 11 mm
Step 2: Derive
Modify Surface Area equations and combine
- [Surface Area of a Cylinder Formula] Factor:
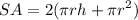
- [Surface Area of a Cylinder Formula] Divide by 2 [Semi-Cylinder]:
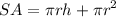
- [Surface Area of a Semi-Cylinder] Substitute in r [Radius Formula]:
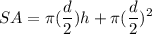
- [Surface Area of a Semi-Cylinder] Evaluate exponents:
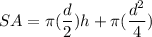
- [Surface Area of a Semi-Cylinder] Multiply:
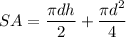
- [Surface Area of a Rectangular Prism] Remove top:
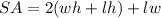
- Combine Surface Area equations:
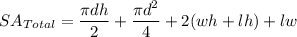
Step 3: Find Surface Area
- Substitute in variables [Combined Surface Area equation]:
![\displaystyle SA_(Total) = (\pi (9 \ mm)(11 \ mm))/(2) + (\pi (9 \ mm)^2)/(4) + 2[(9 \ mm)(6 \ mm) + (11 \ mm)(6 \ mm)] + (11 \ mm)(9 \ mm)](https://img.qammunity.org/2022/formulas/mathematics/high-school/d6e36a4pvhzhnq6ujl0h5bqt73lcpzt7s0.png)
- Evaluate exponents:
![\displaystyle SA_(Total) = (\pi (9 \ mm)(11 \ mm))/(2) + (\pi (81 \ mm^2))/(4) + 2[(9 \ mm)(6 \ mm) + (11 \ mm)(6 \ mm)] + (11 \ mm)(9 \ mm)](https://img.qammunity.org/2022/formulas/mathematics/high-school/bcup3cm8koqs2rm21md95kkgx58nvklwzh.png)
- Multiply:
![\displaystyle SA_(Total) = (99\pi \ mm^2)/(2) + (81\pi \ mm^2)/(4) + 2[54 \ mm^2 + 66 \ mm^2] + 99 \ mm^2](https://img.qammunity.org/2022/formulas/mathematics/high-school/877cjjeqt4n1m3zuwevwtfbowyzsm6x16p.png)
- [Brackets] Add:
![\displaystyle SA_(Total) = (99\pi \ mm^2)/(2) + (81\pi \ mm^2)/(4) + 2[120 \ mm^2] + 99 \ mm^2](https://img.qammunity.org/2022/formulas/mathematics/high-school/zgonlyvhldpcplouhx2gn4pjcttp8zbtdp.png)
- Multiply:
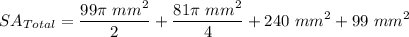
- Add: