Question

Gavin needs to fill the fish tank below with water. The directions state that the water level should be 2 inches below the top of the tank. Write an expression to show the volume of water Gavin needs to fill the tank according to the directions.

Answer 1

See explanation

Explanation:

The question is incomplete; So, I will solve the question generally.

Assume the following;

`l \to length`

`w \to width`

`h \to height`

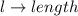
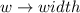
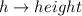
Since the water level must be 2 inches below the tank height, the water height is:

`H \to h - 2`

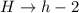
So, the water volume is:

`Volume = l * w * H`

`Volume = l * w * (h - 2)`

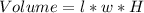
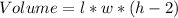
Hence, the expression is:

`Volume = l * w * (h - 2)`

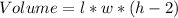
Assume that:

`l = 5; w = 10; h = 8`

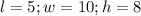
The volume becomes:

`Volume = 5 * 10 * (8 - 2)`

`Volume = 5 * 10 * 6`

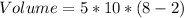
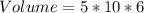
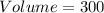`Volume = 300` cubic units