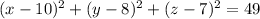Question

Find an equation of the largest sphere with center (10, 8 , 7) that is contained completely in the first octant.

Answer 1

The equation of the largest sphere with center (10, 8, 7) that is contained completely in the first octant is
`(x-10)^(2) + (y - 8)^(2) + (z - 7)^(2) = 49`.

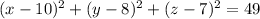Explanation:

A sphere is described by its radius and center, the radius of the largest sphere contained in the first octant are determined by the least distance of the center with respect to an orthogonal axis, that is:

Distance regarding x-axis:

`d_(x) = 10 - 0`

`d_(x) = 10`

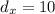
Distance regarding y-axis:

`d_(y) = 8 - 0`

`d_(y) = 8`

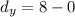
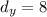
Distance regarding z-axis:

`d_(z) = 7 - 0`

`d_(z) = 7`

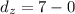
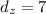
Hence, the radius of the sphere must have a measure of 7. The equation of the sphere is represented by the following geometric locus:

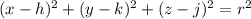`(x-h)^(2) + (y-k)^(2) + (z - j)^(2) = r^(2)` (1)

Where:

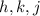`h, k, j` - Coordinates of the center.

`r` - Radius of the sphere.

If we know that
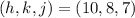`(h,k,j) = (10, 8, 7)` and
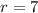`r = 7`, then the equation of the largest sphere with center (10, 8, 7) that is contained completely in the first octant is:

`(x-10)^(2) + (y - 8)^(2) + (z - 7)^(2) = 49`