Understanding Concept :-
Let us consider a quadratic equation αx² + βx + c = 0, then nature of roots of quadratic equation depends upon Discriminant (D) of the quadratic equation.
- If Discriminant, D > 0, then roots of the equation are real and unequal.
- If Discriminant, D = 0, then roots of the equation are real and equal.
- If Discriminant, D < 0, then roots of the equation are unreal or complex or imaginary.
Where,
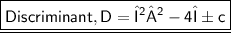
Given Equation:-
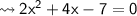
Now,
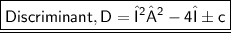
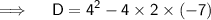
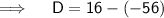
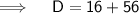

Since, Discriminant, D > 0, then roots of the equation are real and distinct.