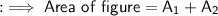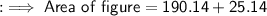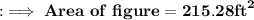Question

Find the total area in the picture. Round to the nearest tenths place.

Answer 1

will recommend to keep in touch with picture as name of sides are based on it!.

It may not get messy so i will divide whole answer into small parts.

Now Let's move to solution :)

`\\ \\`

`\gray{ \bf \dag \frak{Part 1}}`

In this part we will just focus on Semicircle with diameter 22 ft.

Given :-

• Diameter = 22 ft

`\\`

To find:-

• Area of semicircle

`\\`

So first of all let's convert diameter into radius.

we know:-

`\boxed{ \rm{}radius = (Diameter)/(2) }`

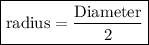
So:-

`\\`

`\hookrightarrow\sf{}radius = (Diameter)/(2)`

`\\`

`\hookrightarrow\sf{}radius = (22)/(2)`

`\\`

`\hookrightarrow\sf{}radius = (2 * 11)/(2)`

`\\`

`\hookrightarrow\sf{}radius = (\cancel2 * 11)/(\cancel2)`

`\\`

`\hookrightarrow\sf{}radius = (11)/(1)`

`\\`

`\hookrightarrow\sf{}radius = 11`

`\\ \\`

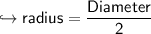
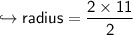
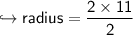
Now let's find area of semicircle!

We know:-

`\boxed{ \rm Area~of~semicircle = \frac{\pi {r}^(2) }{2} }`

`\\`

so:-

`\\`

`\dashrightarrow\sf Area~of~semicircle _1= \frac{\pi {r}^(2) }{2}`

`\\ \\`

`\dashrightarrow\sf Area~of~semicircle _1= \frac{22 * {11}^(2) }{7 * 2} \\`

`\\ \\`

`\dashrightarrow\sf Area~of~semicircle _1= \frac{\cancel{22} * {11}^(\cancel2) }{7 * \cancel2} \\`

`\\ \\`

`\dashrightarrow\sf Area~of~semicircle _1= \frac{11* {11}^(\cancel2) }{7} \\`

`\\ \\`

`\dashrightarrow\sf Area~of~semicircle _1= (1331)/(7) \\`

`\\ \\`

`\dashrightarrow\bf Area~of~semicircle _1= 190.14 \\`

`\\ \\`

`\gray{ \bf \dag \frak{Part 2}}`

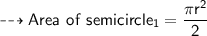
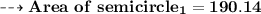
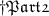
So in this part we will find area of other semicircle.

Now as u can see BC isn't given , but AC and AB are given.

So let's find BC:-

• AC = AB + BC
• BC = AC - AB
• BC = 30 - 22
• BC = 8 ft

`\\`

Now we got the diameter, so let's change it into radius.

we know:-

`\boxed{ \rm{}radius = (Diameter)/(2) }`

`\\`

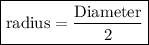
so :-

`\hookrightarrow\sf{}radius = (Diameter)/(2)`

`\\`

`\hookrightarrow\sf{}radius = (8)/(2)`

`\\`

`\hookrightarrow\sf{}radius = (2 * 4)/(2)`

`\\`

`\hookrightarrow\sf{}radius = (\cancel2 * 4)/(\cancel2)`

`\\`

`\hookrightarrow\sf{}radius = 4`

`\\`

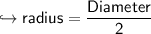
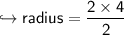
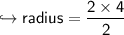
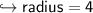
Now let's find area of semicircle!

We know:-

`\boxed{ \rm Area~of~semicircle = \frac{\pi {r}^(2) }{2} }`

`\\`

`\dashrightarrow\sf Area~of~semicircle _2= \frac{\pi {r}^(2) }{2}`

`\\ \\`

`\dashrightarrow\sf Area~of~semicircle _2= \frac{22 * {4}^(2) }{7 * 2} \\`

`\\ \\`

`\dashrightarrow\sf Area~of~semicircle _2= \frac{\cancel{22} * {4}^(\cancel2) }{7 * \cancel2} \\`

`\\ \\`

`\dashrightarrow\sf Area~of~semicircle _2= \frac{11* {4}^(2) }{7} \\`

`\\ \\`

`\dashrightarrow\sf Area~of~semicircle _2= (11* 16)/(7) \\`

`\\ \\`

`\dashrightarrow\sf Area~of~semicircle _2= (176)/(7) \\`

`\\ \\`

`\dashrightarrow\bf Area~of~semicircle _2= 25.14 \\`

`\\ \\`

`\gray{ \bf \dag \frak{Part 3}}`

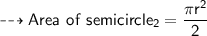
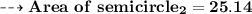
Now Finally in this part we'll add both the areas of these semicircles.

Let :-

• Area of semicircle with diameter AB be A₁
• Area of semicircle with diameter BC be A₂

`\\ \\`

`\sf: \implies Area~of~figure=A_1+A_2 \\`

`\\ \\`

`\sf: \implies Area~of~figure=190.14+25.14 \\`

`\\ \\`

`\bf: \implies Area~of~figure=215.28 {ft}^(2) \\`

`\\ \\`