Question

Find the Total surface area of a cone if it's slant height is 21m and diameter of it's base is 24m.

Don't Spam ​

Answer 1

1244.57 cm²

Explanation:

Given:

• Slant height (l) is 21m
• Diameter (d) is 24m

Hence, radius will be :

➝ diameter/2

➝ 24/2

➝ 12m

`\:`

To Find:

• Total Surface Area (TSA) of the cone.

Solution:

As, we know:

`\star \quad{ \underline{ \green{ \boxed{TSA_((cone)) = \pi r( l+r ) }}}} \quad\star \quad`

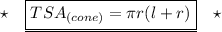
Here,

• π = 22/7
• r = 12m
• l = 21m

`\rightarrow \: (22)/(7) * 12 \: (21 + 12)`

`\rightarrow \: (22)/(7) * 12 \: (33)`

`\rightarrow \: (8712)/(7) {cm}^(2)`

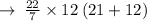
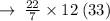
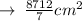
Therefore, Total Surface Area of Cone is 8712/7 cm² or 1244.57cm².

_____________________

Additional Information:

`\footnotesize{\boxed{ \begin{array}{cc} \small\underline{\frak{\pmb{ \red{More \: Formulae}}}} \\ \\ \bigstar \: \bf{CSA_((cylinder)) = 2\pi \: rh}\\ \\ \bigstar \: \bf{Volume_((cylinder)) = \pi {r}^(2) h}\\ \\ \bigstar \: \bf{TSA_((cylinder)) = 2\pi \: r(r + h)}\\ \\ \bigstar \: \bf{CSA_((cone)) = \pi \: r \: l}\\ \\ \bigstar \: \bf{TSA_((cone)) = \pi \: r \: (l + r)}\\ \\ \bigstar \: \bf{Volume_((sphere)) = (4)/(3)\pi {r}^(3) }\\ \\ \bigstar \: \bf{Volume_((cube)) = {(side)}^(3) }\\ \\ \bigstar \: \bf{CSA_((cube)) = 4 {(side)}^(2) }\\ \\ \bigstar \: \bf{TSA_((cube)) = 6 {(side)}^(2) }\\ \\ \bigstar \: \bf{Volume_((cuboid)) = lbh}\\ \\ \bigstar \: \bf{CSA_((cuboid)) = 2(l + b)h}\\ \\ \bigstar \: \bf{TSA_((cuboid)) = 2(lb +bh+hl )}\\ \: \end{array} }}`