Answer:
Approximately
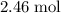 .
.
Step-by-step explanation:
Make use of the molar mass data (
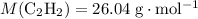 ) to calculate the number of moles of molecules in that
) to calculate the number of moles of molecules in that
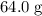 of
of
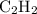 :
:
 .
.
Make sure that the equation for this reaction is balanced.
Coefficient of
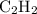 in this equation:
in this equation:
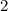 .
.
Coefficient of
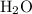 in this equation:
in this equation:
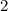 .
.
In other words, for every two moles of
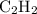 that this reaction consumes, two moles of
that this reaction consumes, two moles of
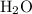 would be produced.
would be produced.
Equivalently, for every mole of
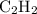 that this reaction consumes, one mole of
that this reaction consumes, one mole of
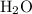 would be produced.
would be produced.
Hence the ratio:
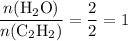 .
.
Apply this ratio to find the number of moles of
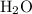 that this reaction would have produced:
that this reaction would have produced:
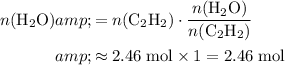 .
.