Hi there! The slope formula is:
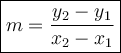
We know that the slope is 4 but we are missing the value of p. (Define m = slope)
What we have now are:
- two ordered pairs (4,2) and (1,p)
- value of slope = 4
We are going to substitute these values and solve the equation for p-term.
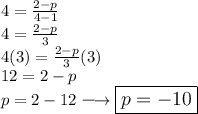
Hence, the value of p is -10.
Next, we have to write the equation of a line in point-slope form. The point-slope form is:
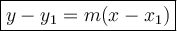
Define that (x1, y1) = ordered pairs
Since we have two given points, we can either use the first point or second point. Both work.
First Point
For our first ordered pairs (4,2), substitute x1 = 4 and y1 = 2 in the equation.
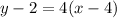
Hence, the equation of a line in point-slope form as in (4,2) is y-2=4(x-4)
Second Point
For our second ordered pairs (1,p), we know that p = -10 from the equation that we solved. Therefore (1,p) = (1,-10). Substitute x1 = 1 and y1 = -10 in the equation.
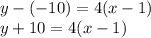
Hence, the equation of a line in point-slope form as in (1,-10) is y+10 = 4(x-1)
Answer
- The value of p is -10 (p = -10)
- y - 2 = 4(x-4) —> use (4,2) to form an equation.
- y + 10 = 4(x-1) —> use (1,-10) to form an an equation.
Both equations work for point-slope form.
Questions can be asked through comment.
Hope this helps, and Happy Learning! :)