Question

What is the first term of a 14-term arithmetic sequence where the last term is −12 and the sum is 42?

A. 6
B. 7
C. 13
D. 18

please explain answer

Answer 1

Answer: D) 18

=========================================

Work Shown:

Here are the variables we're working with

• a = first term
• b = last term (aka nth term)
• n = number of terms
• S = sum of the first n terms

In this case, we know that

• a = unknown (what we want to solve for)
• b = -12
• n = 14
• S = 42

We can use this formula to help find the answer

S = (n/2)*(a+b)

This formula only works for arithmetic sequences

So,

S = (n/2)*(a+b)

42 = (14/2)*(a+(-12))

42 = 7(a-12)

42/7 = a-12

6 = a-12

6+12 = a

18 = a

a = 18 is the first term of this arithmetic sequence

That's why the answer is choice D.

-----------

Side note: your book or your teacher may use the notation
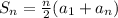`S_n = (n)/(2)(a_1+a_n)` but I figured it would be easier to use 'a' and b in place of
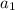`a_1` and
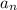`a_n` respectively.