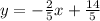Question

If A(2;2) and B(-3;4), determine the equation of AB, in the form y=mx+c​

Answer 1

`y = -(2)/(5)x + (14)/(5)`

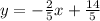
Explanation:

Equation of a line:

The equation of a line has the following format:

`y = mx + c`

In which m is the slope and c is the y-intercept(value of y when x = 0).

A(2;2) and B(-3;4)

When we have two points, the slope is the change in y divided by the change in x. So

Change in y: 4 - 2 = 2

Change in x: -3 - 2 = -5

Slope:
`m = (2)/(-5) = -(2)/(5)`

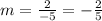
So

`y = -(2)/(5)x + c`

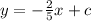
A(2;2)

When
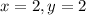`x = 2, y = 2`. We use this to find c.

`y = -(2)/(5)x + c`

`2 = -(2)/(5)(2) + c`

`c = 2 + (4)/(5) = (10)/(5) + (4)/(5) = (14)/(5)`

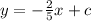
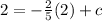
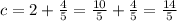
So

`y = -(2)/(5)x + (14)/(5)`