Given:
The equation is:
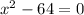
One solutions is 8.
To find:
The other solution of the given equation.
Solution:
We have,
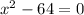
It can be written as:
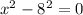
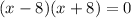
![[\because a^2-b^2=(a-b)(a+b)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/85p639al2fqbkfpvaacm253m69siuprplr.png)
Using zero product property, we get
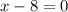 and
and
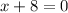
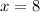 and
and

It is given that the one solutions is 8.
Therefore, the other solution is -8.