Question

Is the ans i got correct?
the total surface area is 33.8cm²
​

Answer 1

Given:

A prism with height 5 cm and equilateral triangular base with side 2 cm.

To find:

The total surface area of the prism.

Solution:

Area of an equilateral triangle is:

`A_1=(√(3))/(4)a^2`

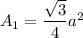
Where, a is the side length.

Putting
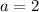`a=2`, we get

`A_1=(√(3))/(4)(2)^2`

`A_1=(√(3))/(4)(4)`

`A_1=√(3)`

`A_1\approx √(3)`

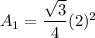
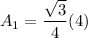
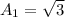
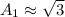
The base and top of the prism are congruent so their area must be equal.

The lateral surface area of the prism is:

`LA=Ph`

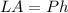
Where, P is the perimeter of the base and h is the height of the prism.

The lateral surface area of the prism is:

`A_2=(2+2+2)5`

`A_2=(6)5`

`A_2=30`

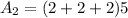
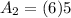
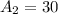
Now, the total surface area is the sum of areas of bases and lateral surface area.

`A=2A_1+A_2`

`A=2(1.73)+30`

`A=3.46+30`

`A=33.46`

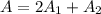
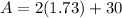
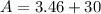
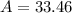
Therefore, the total surface area is 33.46 cm².