Question

(04.06 LC)

The first four terms of a sequence are shown below:
8, 5, 2, -1
Which of the following functions best defines this sequence? (5 points)
f(n) = - 3(n-1) +8; for n 2 1
O f(n) = 3(n-1) +8; for n 2 1
O f(n) = - 5(n-1) +8; for n 2 1
f(n) = 5(n-1) +8; for n 2 1

Answer 1

Given:

The first four terms of a sequence are:

8, 5, 2, -1

To find:

The function that defines the given sequence.

Solution:

We have,

8, 5, 2, -1

The differences between two consecutive terms are:

`5-8=-3`

`2-5=-3`

`-1-2=-3`

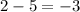
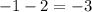
The given sequence has a common difference -3. It means the given sequence is an arithmetic sequence with first term 8 and common difference -3.

The nth terms of an arithmetic sequence is:

`f(n)=a+(n-1)d`, for
`n\geq 1`

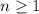
Where, a is the first term and d is the common difference.

Putting
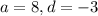`a=8,d=-3`, we get

`f(n)=8+(n-1)(-3)`

`f(n)=8-3(n-1)`

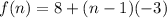
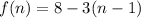
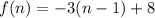`f(n)=-3(n-1)+8`, for
`n\geq 1`

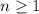
Therefore, the correct option is A.