Question

Solve

`\sf (1)/(p) + (1)/(q) + (1)/(x) = (1)/(p + q + x)`
​

Answer 1

`\displaystyle \begin{cases} \displaystyle {x} _(1) = - p \\ \displaystyle x _(2) = - q \end{cases}`

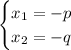
Explanation:

we would like to solve the following equation for x:

`\displaystyle (1)/(p) + (1)/(q) + (1)/(x) = (1)/(p + q + x)`

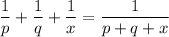
to do so isolate
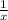`(1)/(x)` to right hand side and change its sign which yields:

`\displaystyle (1)/(p) + (1)/(q) = (1)/(p + q + x) - (1)/(x)`

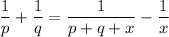
simplify Substraction:

`\displaystyle (1)/(p) + (1)/(q) = (x - (q + p + x))/(x(p + q + x))`

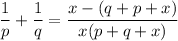
get rid of only x:

`\displaystyle (1)/(p) + (1)/(q) = ( - (q + p ))/(x(p + q + x))`

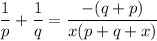
simplify addition of the left hand side:

`\displaystyle (q + p)/(pq) = ( - (q + p ))/(x(p + q + x))`

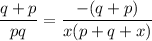
divide both sides by q+p Which yields:

`\displaystyle (1)/(pq) = ( -1)/(x(p + q + x))`

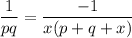
cross multiplication:

`\displaystyle x(p + q + x) = - pq`

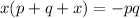
distribute:

`\displaystyle xp + xq + {x}^(2) = - pq`

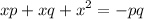
isolate -pq to the left hand side and change its sign:

`\displaystyle xp + xq + {x}^(2) + pq = 0`

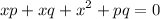
rearrange it to standard form:

`\displaystyle {x}^(2) + xp + xq + pq = 0`

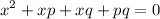
now notice we end up with a quadratic equation therefore to solve so we can consider factoring method to use so

factor out x:

`\displaystyle x( {x}^{} + p ) + xq + pq = 0`

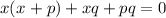
factor out q:

`\displaystyle x( {x}^{} + p ) +q (x + p)= 0`

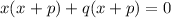
group:

`\displaystyle ( {x}^{} + p ) (x + q)= 0`

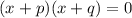
by Zero product property we obtain:

`\displaystyle \begin{cases} \displaystyle {x}^{} + p = 0 \\ \displaystyle x + q= 0 \end{cases}`

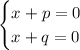
cancel out p from the first equation and q from the second equation which yields:

`\displaystyle \begin{cases} \displaystyle {x}^{} = - p \\ \displaystyle x = - q \end{cases}`

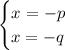
and we are done!