
Given :-
- Adah wants to buy a rug for room that is 19 feet wide and 26 feet long.
- She wants to leave a uniform strip of floor around the rug
- She can only afford to buy 330 sq. feet carpet.
To Find :-
- We have to find the dimensions of the rug .
Let's Begin :-
Here, we have
- The dimensions of Adah room that is 19 feet wide and 26 feet long.
But,
- She wants to leave a uniform strip of floor around the rug.
Therefore,
Let the width of the uniform strip of the floor be x
So, The new dimensions of the room will be

- She can only afford to buy 330 sq.feet
We know that,
Area of rectangle
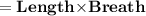
Subsitute the required values,

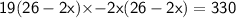



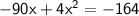
- Arrange the given terms in general quadratic equation that ax² + bx + c = 0
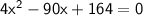
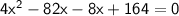
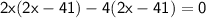
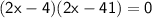
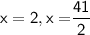
- We can only take only 1 value that is x = 2 because 41/2 will give negative result and dimensions of rectangle can never be negative.
Therefore,
Length of the rug
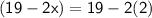
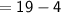

Breath of the rug
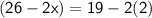
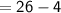
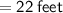
Hence, The dimensions of the rug are 15 feet and 22 feet.