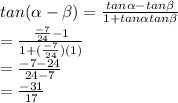Question

Given: α is an angle in the second quadrant, csc α = 25/7; β is an angle in the first quadrant, cos β = √2/2. The value of tan ( α - β ) = _____.

-3/17
29/17
-31/17
15/17

Answer 1

-31/17

Explanation:

csc²α-cot²α=1

cot²α=csc²α-1=(25/7)²-1=(625-49)/49=576/49

α is in 2nd quadrant so cotα is negative.

cot α=-√(576/49)=-24/7

tan α=-7/24

cos β=√2/2

sec β=2/√2=√2

sec²β-tan ²β=1

tan ²β=sec²β-1

tan²β=(√2)²-1=2-1=1

β is in 1st quadrant ,so tan β is positive.

tan β=1

`tan (\alpha -\beta )=(tan \alpha -tan \beta )/(1+tan \alpha tan \beta ) \\=((-7)/(24) -1)/(1+((-7)/(24)) (1)) \\=(-7-24)/(24-7) \\=(-31)/(17)`