Question

use the picture to write each ratio as a simplified fraction (how are you going to find the length of the third side?) show your thinking

Answer 1

See below

Explanation:

to figure out the ratios we must figure out the length of hypotenuse first to do so we can consider Pythagoras theorem given by

`\displaystyle {a}^(2) + {b}^(2) = {c}^(2)`

`\displaystyle \implies c = \sqrt{ {a}^(2) + {b}^(2) }`

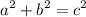
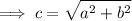
substitute:

`\displaystyle c = \sqrt{ {12}^(2) + {9}^(2) }`

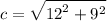
simplify squares:

`\displaystyle c = √( 225 )`

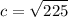
simplify square root:

`\displaystyle c = 15`

now recall that,

• 
  `\displaystyle \sin( \theta) = (opp)/(hypo)`
• 
  `\displaystyle\cos( \theta) = (adj)/(hypo)`
• 
  `\displaystyle \tan( \theta) = (opp)/(adj)`

the ratios with respect to angle w given by

• 
  `\displaystyle \sin( W) = (12)/(15) = (4)/(5)`
• 
  `\displaystyle \cos(W) = (9)/(15) = (3)/(5)`
• 
  `\displaystyle \tan( W) = (12)/(9) = (4)/(3)`

the following ratio with respect to angle X

• 
  `\displaystyle \sin(X) = (9)/(15) = (3)/(5)`
• 
  `\displaystyle \cos(X) = (12)/(15) = (4)/(5)`
• 
  `\displaystyle \tan( X) = (9)/(12) = (3)/(4)`