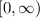Question

Find the domain D and range R of the function f(x)=|9+2x|. (Use symbolic notation and fractions where needed. Give your answers as intervals in the form (∗,∗). Use the symbol [infinity] for infinity and the appropriate type of parenthesis "(", ")", "[", or "]" depending on whether the interval is open or closed.)

Answer 1

Domain of the function 'f' →
`(-\infty,\infty)`

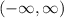
Range of the function 'f' →
`[0,\infty)`

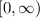
Explanation:

Parent function of an absolute function is,

g(x) = |x|

Domain of the parent function →
`(-\infty,\infty)`

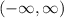
Range of the parent function →
`[0,\infty)`

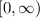
If the function 'g' is vertically stretched by a factor of 2, the new function will be,

h(x) = |2x|

Function 'g' is translated by 9 units to the left, then the new function will be,

f(x) = |2x + 9|

By shifting the parent function on x-axis domain of the function will remain same as of the parent function.

Domain of the function 'f' →
`(-\infty,\infty)`

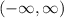
Since, there is no shifting along the y-axis therefore, Range of the function will remain the same as the parent.

Range of the function 'f' →
`[0,\infty)`