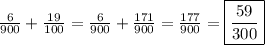Question

(checking answer!)

What is the fraction representation of 0.196 (6 repeating)?

Answer 1

`(59)/(300)`

Explanation:

Recall that
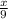`(x)/(9)` returns the decimal
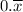`0.\overline{x}`. In this case, we only want the 6 repeating. We can achieve this by finding the fraction excluding the 6 and then adding the repeating fraction with the 6.

0.19 as a fraction is simply
`(19)/(100)`

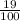
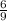`(6)/(9)` returns a repeating digit 6. However, we would like the 6 to be in the thousands place. Since it's already in the tenth place, we will divide the fraction by 100 to put it in the thousands place:
`(6)/(9)\cdot (1)/(100)=(6)/(900)`

Adding these two fractions, we get:

`(6)/(900)+(19)/(100)=(6)/(900)+(171)/(900)=(177)/(900)=\boxed{(59)/(300)}`

Answer 2

49/250 I think I'm not sure though