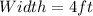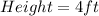Question

A box with a rectangular base and open top must have a volume of 128 f t 3 . The length of the base is twice the width of base. The base needs to be stronger than the sides, so it costs more. The base costs $9 per f t 2 , while the sides only cost $6 per f t 2 . We wish to find the dimensions of the box that minimize the cost of material used.

Answer 1

`Width = 4ft`

`Height = 4ft`

`Length = 8ft`

Explanation:

Given

`Volume = 128ft^3`

`L = 2W`

`Base\ Cost = \$9/ft^2`

`Sides\ Cost = \$6/ft^2`

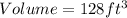
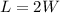
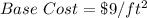
Required

The dimension that minimizes the cost

The volume is:

`Volume = LWH`

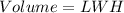
This gives:

`128 = LWH`

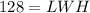
Substitute
`L = 2W`

`128 = 2W * WH`

`128 = 2W^2H`

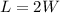
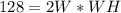
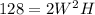
Make H the subject

`H = (128)/(2W^2)`

`H = (64)/(W^2)`

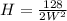
The surface area is:

Area = Area of Bottom + Area of Sides

So, we have:

`A = LW + 2(WH + LH)`

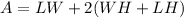
The cost is:

`Cost = 9 * LW + 6 * 2(WH + LH)`

`Cost = 9 * LW + 12(WH + LH)`

`Cost = 9 * LW + 12H(W + L)`

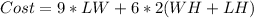
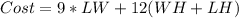
Substitute:
`H = (64)/(W^2)` and
`L = 2W`

`Cost =9*2W*W + 12 * (64)/(W^2)(W + 2W)`

`Cost =18W^2 + (768)/(W^2)*3W`

`Cost =18W^2 + (2304)/(W)`

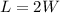
To minimize the cost, we differentiate

`C' =2*18W + -1 * 2304W^(-2)`

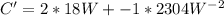
Then set to 0

`2*18W + -1 * 2304W^(-2) =0`

`36W - 2304W^(-2) =0`

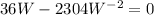
Rewrite as:

`36W = 2304W^(-2)`

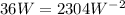
Divide both sides by W

`36 = 2304W^(-3)`

Rewrite as:

`36 = (2304)/(W^3)`

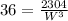
Solve for
`W^3`

`W^3 = (2304)/(36)`

`W^3 = 64`

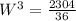
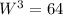
Take cube roots

`W = 4`

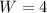
Recall that:

`L = 2W`

`L = 2 * 4`

`L = 8`

`H = (64)/(W^2)`

`H = (64)/(4^2)`

`H = (64)/(16)`

`H = 4`

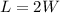
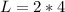
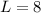
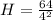
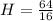
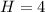
Hence, the dimension that minimizes the cost is:

`Width = 4ft`

`Height = 4ft`

`Length = 8ft`