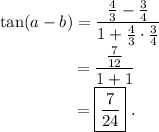Question

Find tan(a-b)

sin a=4/5
tan b=3/4
Give the exact answer, not a decimal approximation.

Answer 1

`(7)/(24)`

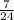
Explanation:

By the Pythagorean Theorem, we know

`\cos^2a=1-\sin^2a`.

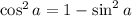With this, we can find
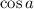`\cos a` by plugging in what we know for
`\sin a`:

`\cos^2a=1-((4)/(5))^2\\~~~~~~~~=1-(16)/(25)\\~~~~~~~~=(9)/(25)`.

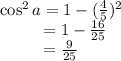Taking the square root, we get

`\cos a=(3)/(5)` .

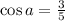Note: there seems to be a problem with the question? It doesn't specify what range
`a` lies in, so we don't know whether
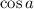`\cos a` is positive or negative. In this case, I assumed it was positive.

From this, we can find
`\tan a`:

`\tan a=(\sin a)/(\cos a)\\~~~~~~~=((4)/(5))/((3)/(5)),`

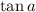so
`\tan a=(4)/(3)`.

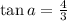Using the
`\tan` difference formula, we know

`\tan (a-b)=(\tan a -\tan b)/(1+\tan a\tan b)` .

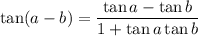Plugging in the values we know for
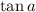`\tan a` and
`\tan b`, we get

`\tan(a-b)=((4)/(3)-(3)/(4))/(1+(4)/(3)\cdot(3)/(4))\\~~~~~~~~~~~~~~=((7)/(12))/(1+1)\\~~~~~~~~~~~~~~=\boxed{(7)/(24)}~.`

Answer 2

Answer: 0.2916666665

Explanation: