Answer:
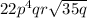
Explanation:
I am interpreting what you wrote as
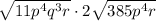 , sorry if that's not what you meant!
, sorry if that's not what you meant!
We rewrite
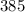 as
as
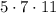 . Since the radicals have the same index, the expression can be written as
. Since the radicals have the same index, the expression can be written as
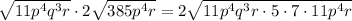 .
.
Multiplying like terms, the expression simplifies to
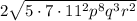 .
.
Taking out the perfect square factors,
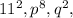 and
and
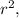 we get
we get
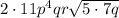 , or
, or
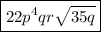 .
.

