Question

Cuale es la distancia entre dos puntos (6,-7)(-2,8)

Answer 1

17

Explanation:

Use the distance formula to determine the distance between the two points.

`d = \sqrt{(x_(2) -x_(1))^(2) + (y_(2) - x_(1))^(2) }`

d = distance

`(x_(1), y_(1))` = coordinates of the first point

`(x_(2), y_(2))` = coordinates of the second point

Answer 2

Answer: The distance between the points (6,-7)(-2,8) is 17.

Explanation:

To calculate the distance between two points, we apply the following formula:

`\boldsymbol{\sf{d=√((x_2-x_1)^2+(y_2-y_1)^2 ) }}`

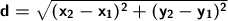
The points are:

• (x₁, y₁) = 6, -7
• (x₂, y₂) = -2. 8

We substitute in the formula and solve:

`\boldsymbol{\sf{d=√((x_2-x_1)^2+(y_2-y_1)^2 ) }}\\ \\ \boldsymbol{\sf{d=√((-2-6)^2+(8-(-7))^2 ) }}\\ \\ \boldsymbol{\sf{d=√((-8)^2+15^2)=√(64+225 ) }}\\ \\ \boldsymbol{\sf{d=√(289)=17 }}`

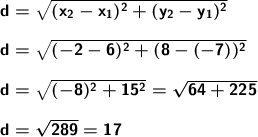
The distance between the points (6,-7)(-2,8) is 17.