Question

Fifteen students from Poppy High School were accepted at Branch University. Of those students, six were offered academic scholarships and nine were not. Mrs. Bergen believes Branch University may be accepting students with lower ACT scores if they have an academic scholarship. The newly accepted student ACT scores are shown here.

Academic scholarship: 25, 24, 23, 21, 22, 20
No academic scholarship: 23, 25, 30, 32, 29, 26, 27, 29, 27

Part A: Do these data provide convincing evidence of a difference in ACT scores between students with and without an academic scholarship? Carry out an appropriate test at the α = 0.02 significance level. (5 points)

Part B: Create and interpret a 98% confidence interval for the difference in the ACT scores between students with and without an academic scholarship. (5 points)

Answer 1

See below for answers and explanations

Explanation:

Part A:

Given:

Pooled sample size:
`n=15`

Sample size (with academic scholarships):
`n_1=6`

Sample size (no academic scholarships):
`n_2=9`

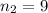
Population standard deviations: Unknown

Sample mean (with academic scholarships):
`\bar{x}=(25+24+23+21+22+20)/(6)=22.5`

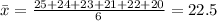
Sample mean (no academic scholarship):
`\bar{x}=(23+25+30+32+29+26+27+29+27)/(9)=27.\bar{5}`

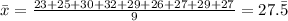
Sample standard deviation (with academic scholarships):
`s_1=1.7078`

Sample standard deviation (no academic scholarships):
`s_2=2.5868`

Degrees of freedom:
`df=n-2=15-2=13`

Significance level:
`\alpha =0.02`

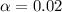
Decide which test is most appropriate to conduct:

Therefore, we will conduct a 2-sample t-test assuming our conditions are satisfied.

List null and alternate hypotheses:

`H_o:\mu_1=\mu_2` -> There's no difference in ACT scores between students with and without an academic scholarship

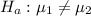`H_a:\mu}_1\\eq\mu_2` -> There's a difference in ACT scores between students with and without an academic scholarship (it's two-sided)

Determine the value of the test statistic:

We will use the formula
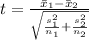`t=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{(s_1^2)/(n_1)+(s_2^2)/(n_2) } }` to compute the test statistic
`t`. Therefore, the test statistic is
`t=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{(s_1^2)/(n_1)+(s_2^2)/(n_2) } }=\frac{27.\bar{5}-22.5}{\sqrt{(1.7078^2)/(6)+(2.5868^2)/(9) } }=4.5592`

Calculate the p-value:

Because the test is two-sided,
`p=2tcdf(4.5592,1e99,13)=2(0.0003)=0.0006`

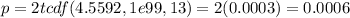
Interpret p-value and conclude test:

Given our significance level is
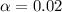`\alpha =0.02`, since
`p<\alpha`, we reject the null hypothesis and conclude that there is significant evidence that suggests that there is a difference in ACT scores between students with and without an academic scholarship (it's more likely that the alternate hypothesis is true)

Part B:

The formula for a confidence interval for the difference in 2 population means is
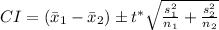`CI=(\bar{x}_1-\bar{x}_2)\pm t^*\sqrt{(s_1^2)/(n_1)+(s_2^2)/(n_2)}}` where
`\bar{x}_1-\bar{x}_2` is the difference of the 2 sample means and
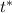`t^*` is the critical score for the desired confidence level.

The critical score for our 98% confidence interval would be
`t^*=invT(0.99,13)=2.6503`

Therefore, our 98% confidence interval for the difference in the ACT scores between students with and without an academic scholarship is
`CI=(27.\bar{5}-22)\pm 2.6503\sqrt{(1.7078^2)/(6)+(2.5868^2)/(9)}}=[2.6167,8.4944]`

This means that we are 98% confident that the true difference in the ACT scores between students with and without an academic scholarship is contained within the interval
`[2.6167,8.4944]`