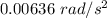Question

A certain CD has a playing time of 74.0 minutes. When the music starts, the CD is rotating at an angular speed of 480 revolutions per minute (rpm). At the end of the music, the CD is rotating at 210 rpm. Find the magnitude of the average angular acceleration of the CD. Express your answer in rad/s2.

Answer 1

Answer:
`0.00636\ rad/s^2`

Step-by-step explanation:

Given

CD has a playing time of
`t=74\ min\ or\ 74* 60\ s`

Initial angular speed of CD is
`480\ rpm`

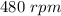
Final angular speed of DC is
`210\ rpm`

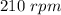
Angular speed, when rpm is given

`\omega =(2\pi N)/(60)`

`\omega_i=(2\pi * 480)/(60)\\\\\Rightarrow \omega_i=16\pi \ rad/s`

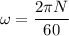
Final speed

`\Rightarrow \omega_f=(2\pi * 210)/(60)\\\\\Rightarrow \omega_f=7\pi \ rad/s`

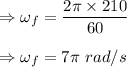
Using equation of angular motion

`\Rightarrow \omega_f=\omega_i+\alpha t`

Insert the values

`\Rightarrow 7\pi =16\pi +\alpha * 74* 60\\\Rightarrow -9\pi =\alpha \cdot (4440)\\\\\Rightarrow \alpha=-(9\pi)/(4440)\\\\\Rightarrow \alpha=-0.00636\ rad/s^2`

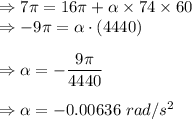
Magnitude of angular acceleration is
`0.00636\ rad/s^2`