Question

In a double-slit arrangement, the slits are separated by a distance equal to 100 times the wavelength of the light passing through the slits. (a) Calculate the angular separation, !, in radians between the central maximum and the 1st order maximum

Answer 1

The conditions for the maximum in the Young's experiment is :

d sin θ = m λ, where m = 0, 1, 2, 3, .....

The angle between the central maximum and the 1st order maximum can be determined by setting the m = 1. So,

d sin θ = λ

`$\theta = \sin^(-1)\left((\lambda)/(d)\right)$`

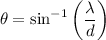
Given : d = 100 λ

`$\theta = \sin^(-1)\left((\lambda)/(100 \lambda)\right)$`

`$\theta = \sin^(-1)\left((1)/(100)\right)$`

`$=0.573^\circ$`

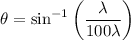
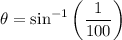
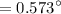
= 0.01 rad