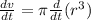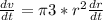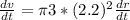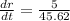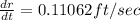Answer:
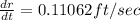
Explanation:
From the question we are told that:
Radius
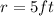
Height
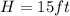
Rate
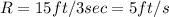
Surface Radius
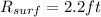
Generally the equation for Volume is mathematically given by
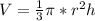
Since radius to height ratio gives
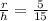
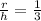

Therefore
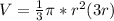

Generally the equation for Change of Volume is mathematically given by