Answer:
The parametric equations represents an ellipse by the rectangular equation
 .
.
Explanation:
We proceed to use the following trigonometric identity to derive an expression in rectangular form:
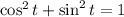 (1)
(1)
Where:
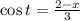 and
and
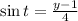
Then, we expand the expression as follows:
 (2)
(2)
The parametric equations represents an ellipse by the rectangular equation
 .
.