Answer:
Explanation:
there is a formula for finding distance,
distance = sqrt [ ( x2-x1)^2 + (y2-y1)^2 ]
where point P1 = (-9.-6)
in the form of (x1,y1)
and point P2 = (-2,-2)
in the form of (x2,y2)
then
distance = sqrt [ (-2-(-9))^2 + (-2-(-6))^2 ]
distance = sqrt [ (-2+9)^2 + (-2+6)^2 ]
distance = sqrt [
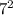 +
+
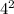 ]
]
distance =
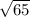
you can leave it in the form of
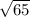 because that's the most accurate , but also can make a close approximation with 8.062257748
because that's the most accurate , but also can make a close approximation with 8.062257748
That's all the places my calculators goes out to, the numbers continue thou.