Question

The City of Irvine upgraded a bicycle lane in a section of road to have a physical barrier between the cyclists as opposed to just a painted white line on the road. They now want to do a study to see if the bicycle lane upgrades have encouraged more people to utilize the bike lane. Before the upgrade, on any given day, it was known that the section of road saw an average of 350 unique cyclists. After the upgrade, they took a random sample of 35 days in the year and counted the number of unique cyclists each day. The average was 405 cyclists with a standard deviation of 25. Test the hypothesis at the 0.05 significance level.

Answer 1

The p-value of the test is 0 < 0.05, which means that there is significant evidence to conclude that more people utilize the bike lane after the change.

Explanation:

Before the upgrade, on any given day, it was known that the section of road saw an average of 350 unique cyclists. Test if more people are using now.

At the null hypothesis, we test if the same number of people is still using, that is, the mean is 350. So

`H_0: \mu = 350`

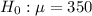
At the alternate hypothesis, we test if this mean increased, that is:

`H_1: \mu > 350`

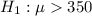
The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.

350 is tested at the null hypothesis:

This means that
`\mu = 350`

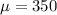
After the upgrade, they took a random sample of 35 days in the year and counted the number of unique cyclists each day. The average was 405 cyclists with a standard deviation of 25.

This means that
`n = 35, X = 405, s = 25`.

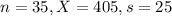Test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (405 - 350)/((25)/(√(35)))`

`t = 13.02`

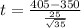
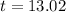
P-value of the test and decision:

The p-value of the test is the probability of finding a sample mean above 405, which is a right-tailed test with t = 13.02 and 35 - 1 = 34 degrees of freedom.

Using a t-distribution calculator, this probability is of 0.

The p-value of the test is 0 < 0.05, which means that there is significant evidence to conclude that more people utilize the bike lane after the change.