Answer:
For equation:
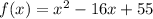
Vertex:
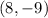
Axis of symmetry, (
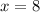 )
)
For equation,
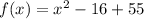
Vertex:
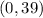
Axis of symmetry, (
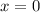 )
)
Explanation:
The x-coordinate of the vertex of a parabola indicates the line of symmetry of the parabola. Thus, to solve this problem, one must find the vertex of the parabola. This can be done through a process called completing the square.
Completing the square is a process that converts a quadratic equation in standard form into vertex form. The first step is to group the linear and quadratic terms. Then factor out the coefficient of the quadratic term. After doing so, add a term to make the group a perfect square trinomial, then balance the equation.
Possibility 1
If the given equation is the following,
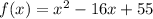
Group,

There is no quadratic term, thus, complete the square,
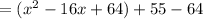
Simplify,
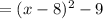
Vertex:
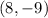
Axis of symmetry, (
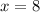 )
)
Possibility 2
If the given equation is the following,
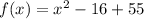
Combine like terms,
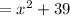
Put in vertex form,
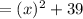
Vertex:
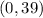
Axis of symmetry, (
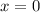 )
)