Question

Find a solution for each variable based on the given information.

If (11+x) is positive, but (4+x) is negative, what is one number x could be?
If (−3+y) is positive, but (−9+y) is negative, what is one number that y could be?
If (−5+z) is positive, but (−6+z) is negative, what is one number that z could be?

Answer 1

1) you can choose: -5, -6, -7, -8, -9, or -10

Explanation:

If you subtract 11 + -5 through -10 you have a positive number. If you subtract 4 + -5 through -10 you have a negative number.

Answer 2

Problem 1)

`-11<x<-4`

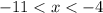
Sample value is -6.

Problem 2:

`3<y<9`

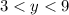
Sample value is 6.

Problem 3:

`5<z<6`

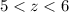
Sample value is 5.5.

Explanation:

We can write inequalities to represent each situation.

Problem 1)

(11 + x) is positive and (4 + x) is negative. In other words:

`11+x>0\text{ and } 4+x<0`

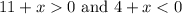
Solving for x yields:

`x>-11\text{ and } x<-4`

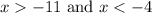
Combining them:

`-11<x<-4`

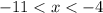
Any values that satisfy this inequality will work.

An example will be -6.

Problem 2)

(-3 + y) is positive and (-9 + y) is negative. Hence:

`-3+y>0\text{ and } -9+y<0`

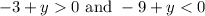
Solving for y yields:

`y>3\text{ and } y<9`

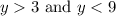
So:

`3<y<9`

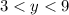
A sample value will be 6.

Problem 3)

(-5 + z) is positive and (-6 + z) is negative. Hence:

`-5+z>0\text{ and } -6+z<0`

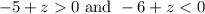
Solving for z yields:

`z>5\text{ and } z<6`

So:

`5<z<6`

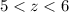
A sample value will be 5.5.