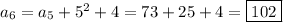Question

7,16,30,49,73,?
find next number in series​

Answer 1

Let A be the first sequence, and denote by
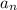`a_n` the n-th term in A.

Consider the forward differences of A :

16 - 7 = 9

30 - 16 = 14

49 - 30 = 19

73 - 49 = 24

Call this sequence of first differences B, so that for n ≥ 1,

`b_n=a_(n+1)-a_n`

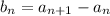
where
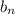`b_n` is the n-th term of B.

Now consider the forward differences of B, which is another sequence we'll call C :

14 - 9 = 5

19 - 14 = 5

24 - 19 = 5

Then if
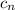`c_n` is the n-th term of C, we have for all n ≥ 1,

`c_n=b_(n+1)-b_n=5`

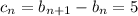
which gives

`b_(n+1) = b_n+5`

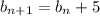
This tells us B is an arithmetic sequence - the first term is 9 and the difference between consecutive terms is 5, so we have for n ≥ 1,

`b_n = 9 + 5(n-1) = 5n + 4`

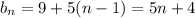
Plug this into the recurrence for A :

`a_(n+1) = a_n + b_n = a_n + 5n + 4`

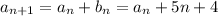
We don't need to solve for
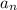`a_n`, fortunately; we just want the next term, which would be

`a_6 = a_5 + 5^2 + 4 = 73 + 25 + 4 = \boxed{102}`