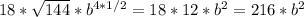Question

Simplify.

Multiply and remove all perfect squares from inside the square roots. Assume b is positive.

Answer 1

216*b^2

Explanation:

first, remember that:

a*√b = √(a^2*b)

√a*√b = √(a*b)

`b^n*b^m = b^(n + m)`

`(b^n)^m = b^(n*m)`

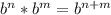
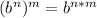
Now, our expression is:

`2*√(8*b^3) *9*√(18*b) = (2*9)*√(8*b^3)*√(18*b)`

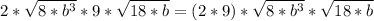
Where in the right I rewrite the expression so it is easier to work.

Now we can use the second property of the above ones, to have:

`18*√(8*b^3*18*b) = 18*\sqrt{(8*18)*b^(3 + 1)} = 18*√(144*b^4)`

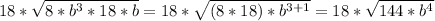
And we know that:

`√(x) = x^(1/2)`

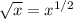
Then:

`18*√(144*b^4) = 18*(144*b^4)^(1/2) = 18*√(144)*(b^4)^(1/2)`

and 12*12 = 144, then:

`18*√(144)*b^(4*1/2) = 18*12*b^2 = 216*b^2`