X^2+10x-39=0 find x Please Please Please Please Please Please Need Help Now

Question

asked Oct 1, 2023 18.8k views

2 Answers

Ilyssa · Answer 1 · 2023-10-01T15:12:20+0000

We are given with the equation x² + 10x - 39 = 0 and need to find x, so let's start ;

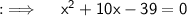
${:\implies \quad \sf x^(2)+10x-39=0}$

By using splitting the middle term method, Rewrite as ;

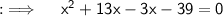
${:\implies \quad \sf x^(2)+13x-3x-39=0}$

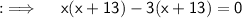
${:\implies \quad \sf x(x+13)-3(x+13)=0}$

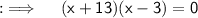
${:\implies \quad \sf (x+13)(x-3)=0}$

So, here either (x + 13) = 0 or (x - 3) = 0, when you equate both of them with 0, you will get x = -13 and x = 3

Hence, The required answer is -13 and 3

Benpage · Answer 2 · 2023-10-05T21:44:56+0000

Answer :

⠀

Explanation :

$\longrightarrow \sf \qquad {x}^(2) + 10x - 39 = 0$

⠀

We have to find the two numbers a and b such that,

$\longrightarrow \sf \qquad a + b = 10$

$\longrightarrow \sf \qquad a b = 39$

⠀

Obviously, the two numbers are 3 and 13.

$\longrightarrow \sf \qquad {x}^(2) - 3x + 13x - 39 = 0$

$\longrightarrow \sf \qquad {x}(x - 3)+ 13(x - 3) = 0$

$\longrightarrow \sf \qquad ({x}+ 13)(x - 3) = 0$

⠀

Whether, the value of x :

$\longrightarrow \sf \qquad {x}+ 13 = 0$

$\longrightarrow \pmb{\bf \qquad {x} = - 13}$

⠀

Whether, the value of x :

$\longrightarrow \sf \qquad {x} - 3 = 0$

${\longrightarrow { \pmb{\bf \qquad {x} = 3}}}$

⠀